题目内容
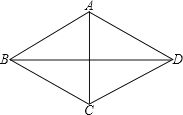
【题目】已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为 .
【答案】4 ![]() 或2
或2 ![]()
【解析】解:连结OA, 
∵AB⊥CD,
∴AM=BM= ![]() AB=
AB= ![]() ×8=4,
×8=4,
在Rt△OAM中,OA=5,
∴OM= ![]() =3,
=3,
当如图1时,CM=OC+OM=5+3=8,
在Rt△ACM中,AC= ![]() =4
=4 ![]() ;
;
当如图2时,CM=OC﹣OM=5﹣3=2,
在Rt△ACM中,AC= ![]() =2
=2 ![]() .
.
所以答案是4 ![]() 或2
或2 ![]() .
.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目