题目内容
如图所示,在四边形ABCD中,∠B+∠D=1800,AB=AD,AC=1,∠ACD=600,则四边形ABCD的面积为 。


过A点分别作AE⊥BC于E,AF⊥CD于F,连接BD,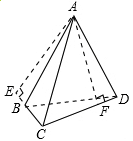
∵∠ADF+∠ABC=180°,且∠ABE+∠ABC=180°,
∴∠ADF=∠ABE,且A,B,C,D四点共圆,
又∠ACD=60°,
∴∠ABD=∠ACD=60°,又AB=AD,
∴△ABD是等边三角形,
∴∠BAD=60°,
∴∠EAF=∠EAB+∠BAF,∠BAD=∠FAD+∠BAF,
∴∠EAF=∠BAD=60°,
∴∠EAC=180°-60°=120°,
∴∠AEC=60°,
∴S△AEC="1/2" EC•AE="1/2" AB•sin60°•AB•cos60°= ,
,
同理S△AEC= ,
,
在△ABE与△ADF中,
∵∠ADF=∠ABE,AB=AD,∠AEB=∠AFD,
∴△AEB≌△AFD,
∴S四边形ABCD=S四边形AECF=S△AEC+S△AEC= +
+ =
= .
.

∵∠ADF+∠ABC=180°,且∠ABE+∠ABC=180°,
∴∠ADF=∠ABE,且A,B,C,D四点共圆,
又∠ACD=60°,
∴∠ABD=∠ACD=60°,又AB=AD,
∴△ABD是等边三角形,
∴∠BAD=60°,
∴∠EAF=∠EAB+∠BAF,∠BAD=∠FAD+∠BAF,
∴∠EAF=∠BAD=60°,
∴∠EAC=180°-60°=120°,
∴∠AEC=60°,
∴S△AEC="1/2" EC•AE="1/2" AB•sin60°•AB•cos60°=
 ,
,同理S△AEC=
 ,
,在△ABE与△ADF中,
∵∠ADF=∠ABE,AB=AD,∠AEB=∠AFD,
∴△AEB≌△AFD,
∴S四边形ABCD=S四边形AECF=S△AEC+S△AEC=
 +
+ =
= .
.
练习册系列答案
相关题目
 中,
中,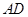 ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
 ;
; 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由.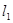 ∥
∥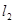 ,它们之间的距离等于a,一块正方形纸板
,它们之间的距离等于a,一块正方形纸板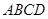 的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.
的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.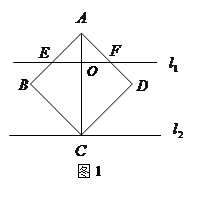
 于O,使得直线
于O,使得直线 、
、 相交于E、F.求证:①BE="OE" ②
相交于E、F.求证:①BE="OE" ②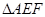 的周长等于
的周长等于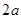 ;
;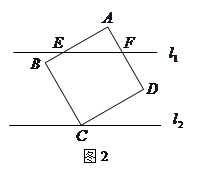
 、CD相交于G,H,设
、CD相交于G,H,设 AEF的周长为
AEF的周长为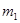 ,
,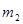 ,试问
,试问
 之间存在着什么关系?试直接写出你的结论(不需证明).
之间存在着什么关系?试直接写出你的结论(不需证明).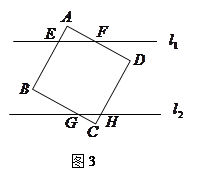
 90°,BD⊥DC,BD=DC,CE平分
90°,BD⊥DC,BD=DC,CE平分 ,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②
,交AB于点E,交BD于点H,EN∥DC交BD于点N,下列结论:①BH=DH;②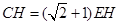 ;③
;③ ,其中正确的是( )
,其中正确的是( )



