题目内容
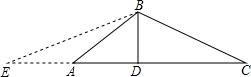
如图，在△ABC中，∠ABC=120°，BD是AC边上的高，若AB+AD=DC，则∠C等于（ ）
| A．10° | B．20° | C．30° | D．40° |
如图，延长DA到E，使AE=AB，
∵AB+AD=DC，
∴AE+AD=AB+AD=DC，
又∵BD是AC边上的高，
∴BD是CE的垂直平分线，
∴BC=BE，
根据等边对等角，∠C=∠E，∠E=∠ABE，
根据三角形的外角性质，∠BAD=∠E+∠ABE=2∠C，
在△ABC中，∠BAD+∠C+∠ABC=180°，
∴2∠C+∠C+120°=180°，
解得∠C=20°．
故选B．
∵AB+AD=DC，
∴AE+AD=AB+AD=DC，
又∵BD是AC边上的高，
∴BD是CE的垂直平分线，
∴BC=BE，
根据等边对等角，∠C=∠E，∠E=∠ABE，
根据三角形的外角性质，∠BAD=∠E+∠ABE=2∠C，
在△ABC中，∠BAD+∠C+∠ABC=180°，
∴2∠C+∠C+120°=180°，
解得∠C=20°．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
