题目内容
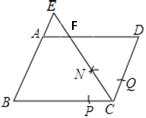
【题目】如图，在平行四边形ABCD中，AB=2，BC=3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于
PQ的长为半径画弧，两弧相交于点N，射线CN交AD与点F，交BA的延长线于点E，则三角形CDF与四边形AFCB的面积比是（ ）
A.2B.C.
D.
【答案】B
【解析】
根据作法可得EC平分∠BCD，可求得AE的长，利用△AEF与△CDF及△BEC的面积比可求解．
由题意可知CE是∠BCD的平分线，
∴∠BCE=∠DCE．
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠DCE=∠E，∠BCE=∠AEC，
∴BE=BC=3，
∵AB=2，
∴AE=BE-AB=1，
∵AE∥CD
∴△AEF∽△DCF
∴
∵△AEF∽△BEC
∴
∴
∴
故选：B
练习册系列答案
培优三好生系列答案
相关题目
