题目内容
【题目】拓展与探索:如图,在正△ABC中,点E在AC上,点D在BC的延长线上.
(1)如图1,AE=EC=CD,求证:BE=ED;
(2)如图2,若E为AC上异于A、C的任一点,AE=CD,(1)中结论是否仍然成立?为什么?
(3)若E为AC延长线上一点,且AE=CD,试探索BE与ED间的数量关系,并证明你的结论.

【答案】(1)证明见解析;(2)成立,理由见解析;(3)BE=ED,证明见解析.
【解析】
(1)根据等边三角形的性质得到∠EBC=![]() ∠ABC=30°,根据等腰三角形的判定定理证明;
∠ABC=30°,根据等腰三角形的判定定理证明;
(2)过点E作EF∥BC,证明△EFB≌△DCE,根据全等三角形的性质证明;
(3)过点E作EF∥AB,证明△BCE≌△DFE,根据全等三角形的性质证明.
解:(1)∵△ABC是等边三角形,AE=CE,
∴BE平分∠ABC,
∴∠EBC=![]() ∠ABC=30°,
∠ABC=30°,
∵∠ACB=60°,
∴∠ECD=120°,
∵CE=CD,
∴∠D=∠CED=30°,
∴∠EBC=∠D=30°,
∴BE=ED;
(2)成立,
理由如下:过点E作EF∥BC,交AB于F,
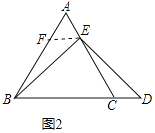
∵△ABC是等边三角形,
∴△AEF是等边三角形,AF=AE=EF,
∴∠BFE=∠ECD=120°,BF=EC,
∵AE=CD,
∴EF=CD,
在△EFB和△DCE中,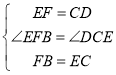 ,
,
∴△EFB≌△DCE(SAS)
∴BE=ED;
(3)结论:BE=ED.
理由如下:如图3,过点E作EF∥AB,交CD于F,
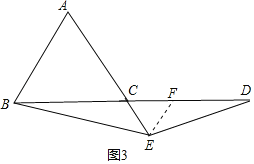
则△CEF是等边三角形,
∴CF=CE=EF,∠BCE=∠DFE=120°,
∵AE=CD,
∴AE﹣CE=CD﹣CF,即AC=FD,
∵AC=BC,
∴BC=FD,
在△BCE和△DFE中,
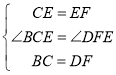 ,
,
∴△BCE≌△DFE(SAS),
∴BE=ED.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目




