题目内容
【题目】某中学举行了一次“奥运会”知识竞赛,赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:
分数段 | 频数 | 频率 |
第一组:60≤x<70 | 30 | 0.15 |
第二组:70≤x<80 | m | 0.45 |
第三组:80≤x<90 | 60 | n |
第四组:90≤x<100 | 20 | 0.1 |
请根据以图表提供的信息,解答下列问题: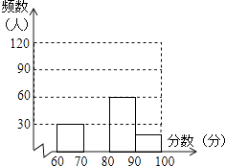
(1)写出表格中m和n所表示的数:m= , n=;
(2)补全频数分布直方图;
(3)抽取部分参赛同学的成绩的中位数落在第组;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
【答案】
(1)90;0.3
(2)解:如图:
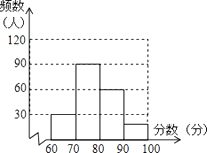
(3)二
(4)解:获奖率= ![]() ×100%=40%.
×100%=40%.
答:获奖率是40%
【解析】解:(1)总人数=30÷0.15=200人, m=200﹣30﹣60﹣20=90,
n=1﹣0.15﹣0.45﹣0.1=0.3;(3)由于总数有200人,中位数应为第100、101名的平均数,而第一组有30人,第二组有90人,故中位数落在第二组内;
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图).

练习册系列答案
相关题目