题目内容
【题目】如图，点A、B、C、D在坐标轴上，直线AB与直线CD：y=2x+2相交于点E（a，﹣3），连接BC，其中B（0，﹣5）．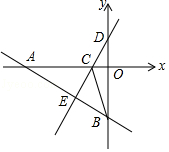 
（1）求直线AB的解析式；
（2）求△BCE的面积．
【答案】
（1）解：当y=﹣3时，2x+2=﹣3，
解得x=﹣ 
，即E（﹣ ，﹣3）．
设AB的解析式y=kx+b，将B，E点坐标代入，得
，
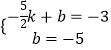解得 
，
直线AB的解析式y=﹣4x﹣5；
（2）解：当y=0时﹣4x﹣5=0，解得x=﹣ 
，即A（﹣ ，0），
当y=0时，2x+2=0，解得x=﹣1，即C（﹣1，0），
S△BCE=S△ABO﹣SACE﹣S△BCO
= 
× ×5﹣ × 
×3﹣ ×1×5
= 
﹣ 
﹣ 
= ．
【解析】（1）根据自变量与函数值得对应关系，可得E点坐标，根据待定系数法，可得答案；（2）根据自变量与函数值的对应关系，可得A，C，E点坐标，根据面积的和差，可得答案．
练习册系列答案
相关题目
【题目】某中学举行了一次“奥运会”知识竞赛，赛后抽取部分参赛同学的成绩进行整理，并制作成图表如下：
分数段 | 频数 | 频率 |
第一组：60≤x＜70 | 30 | 0.15 |
第二组：70≤x＜80 | m | 0.45 |
第三组：80≤x＜90 | 60 | n |
第四组：90≤x＜100 | 20 | 0.1 |
请根据以图表提供的信息，解答下列问题：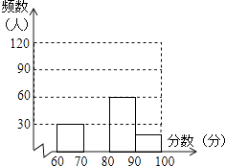
（1）写出表格中m和n所表示的数：m= ， n=；
（2）补全频数分布直方图；
（3）抽取部分参赛同学的成绩的中位数落在第组；
（4）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？