题目内容
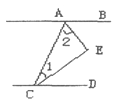
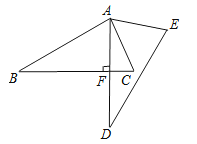
【题目】如图，在平行四边形ABCD中，AB=6，AD=8，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于G，BG=4 
，则四边形AECD的周长为（ ） 
A.20
B.21
C.22
D.23
【答案】C
【解析】解：∵四边形ABCD是平行四边形， ∴BC=AD=9，CD=AB=6，AD∥BC，
∴∠DAE=∠AEB，
∵AE平分∠BAD，
∴∠DAE=∠BAE，
∴∠BAE=∠BEA，
∴BE=AB=6，
∴EC=BC﹣BE=3，
∵BG⊥AE，
∴AG=EG= 
= 
=2，
∴AE=AG+EG=4，
∴四边形AECD的周长为：AD+CD+CE+AE=9+6+3+4=22．
故选：C．
【考点精析】通过灵活运用平行四边形的性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分即可以解答此题．
练习册系列答案
相关题目
【题目】某中学举行了一次“奥运会”知识竞赛，赛后抽取部分参赛同学的成绩进行整理，并制作成图表如下：
分数段 | 频数 | 频率 |
第一组：60≤x＜70 | 30 | 0.15 |
第二组：70≤x＜80 | m | 0.45 |
第三组：80≤x＜90 | 60 | n |
第四组：90≤x＜100 | 20 | 0.1 |
请根据以图表提供的信息，解答下列问题：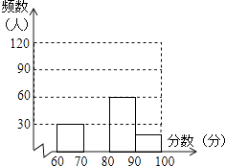
（1）写出表格中m和n所表示的数：m= ， n=；
（2）补全频数分布直方图；
（3）抽取部分参赛同学的成绩的中位数落在第组；
（4）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？
