题目内容
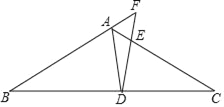
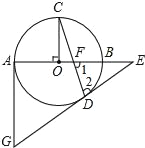
【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
【答案】(1)证明见解析(2)6
【解析】试题分析:(1)连接OD,因为DE为⊙O的切线,所以OD⊥DE,又OC⊥OB,然后根据互余的关系可证∠1=∠2;(2)由(1)中∠1=∠2可得EF=ED,设DE=x,在Rt△ODE中,由勾股定理求得x =4,然后证Rt△EOD∽Rt△EGA.可求出AG的长.
试题解析:(1)证明:如图,连接OD,
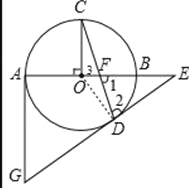
∵DE为⊙O的切线,∴OD⊥DE.∴∠ODE=90°,即∠2 ∠ODC=90°,∵OC=OD,∴∠C=∠ODC.∴∠2 ∠C=90°.∵OC⊥OB,∴∠C ∠3=90°.∴∠2=∠3,∵∠1=∠3,∴∠1=∠2.
(2)∵OF:OB=1:3,⊙O的半径为3,∴OF=1.∵∠1=∠2,∴EF=ED,在Rt△ODE中,OD=3,设DE=x,则EF=x,OE=1+x,所以![]() ,解得x =4.∴DE=4,OE=5.
,解得x =4.∴DE=4,OE=5.
∵AG为⊙O的切线,∴AG⊥AE.∴∠GAE=90°.∴∠ODE=∠GAE,∵∠OED=∠GEA,∴Rt△EOD∽Rt△EGA. ![]() 解得AG=6.
解得AG=6.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
(1)计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
(2)小颖说:“根据实验得出,出现![]() 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?