题目内容
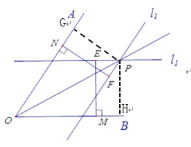
【题目】小明在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图.
(1)在![]() 的内部任取一个点E,过点E作EM⊥OB;
的内部任取一个点E,过点E作EM⊥OB;
(2)在边![]() 上取一点N,作NF⊥OA于点N,且NF=EM;
上取一点N,作NF⊥OA于点N,且NF=EM;
(3)过点E作直线l1∥OB,过点F作直线l2∥OA,l1 与l2交于点![]() ;
;
(4)画射线![]() .
.
则射线![]() 为
为![]() 的平分线.
的平分线.

根据小明的画法回答下面的问题:
(1)小明作l1∥OB,l2∥OA的目的是___________________________________________;
(2)l1 与l2交于点![]() ,则射线
,则射线![]() 为
为![]() 的平分线的依据是__________________________.
的平分线的依据是__________________________.
【答案】利用平行线间的距离处处相等 到角两边距离相等的点在角的平分线上.
【解析】
(1)作l1∥OB,l2∥OA的目的是:利用平行线间的距离处处相等;
(2)过点P作PG⊥OA于G,PH⊥OB于H,再根据l1∥OB,EM⊥OB得出PH= EM;再根据 l2∥OA,NF⊥OA,得出PG=FN,再根据NF=EM,得出PG=PH,根据到角两边距离相等的点在角的平分线上,从而得出射线![]() 为
为![]() 的平分线.
的平分线.
(1)作l1∥OB,l2∥OA的目的是利用平行线间的距离处处相等;
故答案为: 利用平行线间的距离处处相等;
(2)过点P作PG⊥OA于G,PH⊥OB于H,
∵l1∥OB,EM⊥OB,∴PH= EM;
∵l2∥OA,NF⊥OA, ∴PG=FN
∵NF=EM,∴PG=PH,
∴射线![]() 为
为![]() 的平分线(到角两边距离相等的点在角的平分线上).
的平分线(到角两边距离相等的点在角的平分线上).
故答案为: 到角两边距离相等的点在角的平分线上.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】(1)根据下表回答:
| 1 | 1.7 | 1.73 | 1.74 | 1.8 | 2 |
| 1 | 2.89 | 2.9929 | 3.0276 | 3.24 | 4 |
①![]() 的平方根是_____________;
的平方根是_____________;
②由表可知,![]() 在表中哪两个相邻的数之间(小数部分是两位小数)?
在表中哪两个相邻的数之间(小数部分是两位小数)?
(2)如图,在平面直角坐标系中,已知三点![]()
![]()

①三角形![]() 的面积是_______
的面积是_______
②分别将![]() 三点的横坐标乘
三点的横坐标乘![]() ,纵坐标加
,纵坐标加![]() ,记坐标变换后
,记坐标变换后![]() 所对的点分别为
所对的点分别为![]() 在坐标系中画出以这三点为顶点的三角形
在坐标系中画出以这三点为顶点的三角形![]()