题目内容
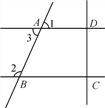
【题目】如图,已知AB∥CD;
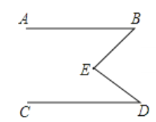
(1)你能找出∠B∠D∠BED的关系吗?
(2)如果∠B=46°,∠D=58°,则∠BED的度数是多少?
【答案】(1)∠BED=∠B+∠D;(2)104°
【解析】
(1)过点E作EF∥AB,根据平行于同一条直线的两直线平行可得EF∥AB∥CD,然后根据平行线的性质可得∠B=∠BEF,∠D=∠DEF,然后根据角的关系和等量代换即可得出结论;
(2)根据(1)的结论代入各角的度数即可求出结论.
解:(1)∠BED=∠B+∠D,理由如下
过点E作EF∥AB

∵AB∥CD
∴EF∥AB∥CD
∴∠B=∠BEF,∠D=∠DEF
∴∠BED=∠BEF+∠DEF=∠B+∠D
(2)∵∠BED=∠B+∠D,∠B=46°,∠D=58°,
∴∠BED=46°+58°=104°

练习册系列答案
相关题目