Question

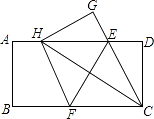
【题目】如图，已知ABCD的四个内角的平分线分别相交于点E、F、G、H，连接AC．若EF=2，FG=GC=5，则AC的长是（　　）

A. 12 B. 13 C. D.

Answer 1

【答案】B

【解析】如图，设AC与DF交于M，AC与EH交于N，

∵四边形ABCD是平行四边形，ABCD的四个内角的平分线分别相交于点E、F、G、H，

∴易证四边形EFGH是矩形，△ABE≌△CDG，△AEN≌△CGM，

∴FG=EH=CG=5，EF=GH=2，CH=7，EN=GM，CM=AN，

∵EH=FG，∴FM=NH，设GM=EN=x，则HN=FN=5﹣x，∵GM∥HN，∴，

∴，∴x=，

在Rt△CMG中，CM=AN==，

在Rt△CNH中，CN==，

∴AC=AN+CN=+=13，

故选B．