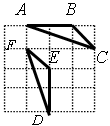
题目内容
如图1,△ABC的边BC在直线 上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP.
(1)将△EFP沿直线 向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
AP BQ,AP BQ; (4分)
(2)将△EFP沿直线 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)
 上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP.(1)将△EFP沿直线
 向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)AP BQ,AP BQ; (4分)
(2)将△EFP沿直线
 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)
(1)BQ=AP,BQ⊥AP.
(2)关系仍然成立:BQ=AP,BQ⊥AP.间解析
(2)关系仍然成立:BQ=AP,BQ⊥AP.间解析
试题分析:(1)延长BQ交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠CBQ=∠CAP,又∠CBQ+∠BQC=90°,所以∠CAP+∠AQM=90°,从而得到BQ⊥AP;
(2)延长QB交AP于点M,根据等腰直角三角板的每一个锐角都是45°可得∠EPF=45°,根据对顶角相等得到∠CPQ=45°,然后求出∠CQP=45°,根据等角对等边的性质求出CQ=CP,然后利用边角边定理证明△BCQ与△ACP全等,再根据全等三角形对应边相等,即可证明BQ=AP,对应角相等可得∠BQC=∠APC,又∠CBQ+∠BQC=90°,所以∠PBM+∠APC=90°,从而得到BQ⊥AP.
点评:本题要求熟练掌握等腰直角三角形的两直角边相等,每一个锐角都是45°的性质,全等三角形的判定与性质,题目不比较复杂但思路比较清晰,此类题目一般都是下一问继续沿用第一问的证明思路进行求解.

练习册系列答案
相关题目

 处6米处折断倒下,量得树梢
处6米处折断倒下,量得树梢 处与树底
处与树底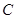 处的长是8米,树干
处的长是8米,树干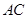 与地面
与地面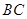 垂直.试通过计算求出这棵大树原来的高度.
垂直.试通过计算求出这棵大树原来的高度.