题目内容
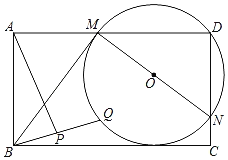
【题目】已知锐角△ABC中，AB＝AC，边BC长为6，高AD长为4，正方形PQMN的两个顶点在△ABC一边上，另两个顶点分别在△ABC的另两边上，则正方形PQMN的边长为（ ）
A.
B.或
C.或
D.或
【答案】B
【解析】
分两种情形：如图1中，当正方形的边QM在BC上时，设AD交PN于K，设正方形的边长为x，如图2中，当正方形的边QM在AB边上时，作CH⊥AB于H交PN于K，设正方形的边长为x，分别利用相似三角形的性质构建方程解决问题即可．
解：如图1中，当正方形的边QM在BC上时，设AD交PN于K，设正方形的边长为x，
∵PN∥BC，
∴△APN∽△ABC，
∴
＝
，
∴
＝
，
解得x＝
；
如图2中，当正方形的边QM在AB边上时，作CH⊥AB于H交PN于K．设正方形的边长为x，
∵AB＝AC，AD⊥BC，
∴BD＝CD＝3，
∵AD＝4，
∴AB＝
＝
＝5，
∵
BCAD＝ABCH，
∴CH＝
，
∵PN∥AB，
∴△CPN∽△CAB，
∴
＝
，
∴
＝
，
解得x＝
，
综上所述，正方形的边长为或；
故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
