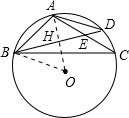
题目内容
如图，已知四边形ABCD的外接圆⊙O的半径为2，对角线AC与BD的交点为E，AE=EC，AB=
AE，且BD=2
，求四边形ABCD的面积．
| 2 |
| 3 |
∵AE=EC，AB=
AE，
∴AB2=2AE2=AE•AC，
∴AB：AC=AE：AB，
又∠EAB=∠BAC，
∴△ABE∽△ACB，
∴∠ABE=∠ACB，
从而AB=AD．
连接AO，交BD于H，连接OB，
∵AB=AD，
∴AO⊥BD，
∴BH=HD，
BO=2，BH=
，
则BH=HD=
．
∴OH=
=
=1，AH=OA-OH=2-1=1．
∴S△ABD=
BD•AH=
×2
×1=
，
∵E是AC的中点，∴S△ABE=S△BCE，
S△ADE=S△CDE，∴S△ABD=S△BCD，
∴S四边形ABCD=2S△ABD=2
．
| 2 |
∴AB2=2AE2=AE•AC，
∴AB：AC=AE：AB，
又∠EAB=∠BAC，
∴△ABE∽△ACB，
∴∠ABE=∠ACB，
从而AB=AD．
连接AO，交BD于H，连接OB，
∵AB=AD，
∴AO⊥BD，
∴BH=HD，
BO=2，BH=
| 3 |
则BH=HD=
| 3 |
∴OH=
| OB2-BH2 |
| 4-3 |
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵E是AC的中点，∴S△ABE=S△BCE，
S△ADE=S△CDE，∴S△ABD=S△BCD，
∴S四边形ABCD=2S△ABD=2
| 3 |
练习册系列答案
浙江名校名师金卷系列答案
相关题目
