��Ŀ����
����Ŀ���������� ABCD ����ͼ 1�������»��֣�
��1�λ��֣��ֱ�����������ABCD�Աߵ��е㣨��ͼ2�������߶�HF��EG�����ǽ��ڵ�M����ʱͼ2�й���5�������Σ�
��2�λ��֣���ͼ2 ���Ͻ�������AEMH�������֣���ͼ3����ͼ3 �й���9�������Σ�
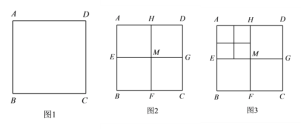
��1����ÿ�ζ������Ͻǵ����������λ�����ȥ�����100�λ��ֺ�ͼ�й��� �������Σ�
��2������������ȥ���ڼ��λ��ֺ�����805��������?д��������̣�
��3�������ַ����ܷ�������ABCD���ֳ���2015�������ε�ͼ�Σ�����ܣ�������ǵڼ��λ��֣�������ܣ���˵�����ɣ�
��4�������ԭ�����εı߳�Ϊ1��ͨ�����ϵطָ�����Ϊ1�������Σ�����������ϵ�ͼ���ͼ������ؽ�����������Ժ����õ�һЩ������������̽������������ʽ�Ľ���ɣ�
���� ![]() ���� ֱ��д���𰸼��ɣ�
���� ֱ��д���𰸼��ɣ�
���𰸡���1��401����2���� 201 �λ��ֺ����� 805�������Σ���3�����ܣ���4��![]()
��������
��1���ɵ�һ�οɵ�5�������Σ��ڶ��οɵ�9�������Σ������οɵ�13�������Σ��ɵù��ɣ���n�οɵã�4n��1���������Σ��̶���ô𰸣�
��2���ɹ��ɿɵ÷���4n��1��805���̶���ô𰸣�
��3���ɹ��ɿɵ�4n��1��2015������nΪ����������ô𰸣�
��4������ɿ������漸����������⣬������ô𰸣�
��1���ߵ�һ�οɵ�5�������Σ��ڶ��οɵ�9�������Σ������οɵ�13�������Σ�
���n�οɵã�4n��1���������Σ�
���100�οɵ������Σ�4��100��1��401��������
�ʴ�Ϊ��401��
��2����������ã�4n��1��805��
��ã�n��201��
���201�λ��ֺ�����805�������Σ�
��3�����ܣ�
��4n��1��2015��
��ã�n��503.5��
��n����������
��ܽ���������ABCD���ֳ���2015�������ε�ͼ�Σ�
��4���������ã�
![]()
��![]()
��![]()
��![]() ��
��

 һ����������ϵ�д�
һ����������ϵ�д�