题目内容
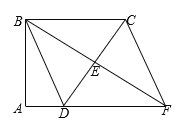
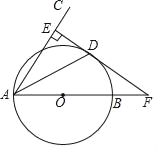
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,过点D作DE⊥AC于E.
(1)求证:ED是⊙O的切线;
(2)若ED,AB的延长线相交于F,且AE=5,EF=12,求BF的长.
【答案】(1)证明见解析;(2)BF=![]() .
.
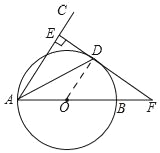
【解析】试题分析:(1)连接OD,推出∠ODA=∠OAD=∠EAD,推出OD∥AE,推出OD⊥DE,根据切线的判定推出即可;
(2)在Rt△AEF中,根据勾股定理求得AF=13,设⊙O的半径为r,则有OD=r,OF=13﹣r,BF=AF﹣AB=13﹣2r,通过证明△OFD∽△AFE,根据相似三角形对应边成比例进而求得r的值即可得..
试题解析:(1)如图,∵DE⊥AC,
∴∠AEF=90°
连接OD,
∴OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB,
∴∠DAE=∠ODA,
∴OD∥AE,
∴∠ODF=∠AEF=90°,
∴OD⊥EF,
∵点D在⊙O上,
∴ED是⊙O的切线;
(2)在Rt△AEF中,根据勾股定理得,AF=![]() =13,
=13,
设⊙O的半径为r,
∴OD=r,OF=13﹣r,BF=AF﹣AB=13﹣2r,
由(1)知,OD∥AE,
∴△OFD∽△AFE,
∴![]() ,
,
∴![]() ,
,
∴r=![]() ,
,
∴BF=13﹣r=![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
【题目】嘉兴某校组织了“垃圾分类”知识竞赛活动,获奖同学在竞赛中的成绩绘成如下图表,
根据图表提供的信息解答下列问题:
垃圾分类知识竞赛活动成绩统计表
分数段 | 频数 | 频数频率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
(1)求本次获奖同学的人数;
(2)求表中x,y的数值:并补全频数分布直方图.