题目内容
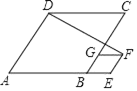
【题目】如图，AB是⊙O的直径，AD、BD是⊙O的弦，且∠PDA=∠1，过点B的切线BE与PD的延长线交于点E．把△PDA沿AD翻折，点P正好落在⊙O的F点上．
（1）证明：PD是⊙O的切线；
（2）求证：DF∥BE；
（3）若PA=2，求四边形BEDF的面积．
【答案】（1）（2）见解析；（3）
【解析】试题分析： 
连接OD． 
根据等量代换得
根据直径所对的圆周角是直角得
即可得到
，即可证明.
由
得
=
,根据垂径定理的推论可得
又BE是切线，即可证明.
根据
可以求出
的长度，证明四边形BEDF是菱形，根据面积公式计算即可.
试题解析：证明：连接OD．
∵
∴
∵
∴
∴
∵AB是直径，
∴
∴
，
∴
∴PD是
的切线．
（2）设AB交DF于H．
∵
∴
=
,
∴
∵BE是切线，
∴
，
∴DF∥BE．
（3）
∴
∴
∵
∴
∵
∴
易证四边形BEDF是菱形，面积
练习册系列答案
相关题目
