题目内容
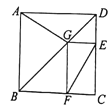
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
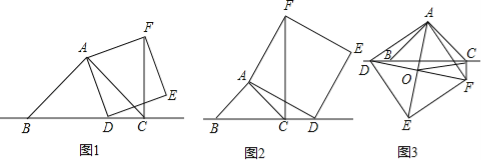
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
【答案】(1)证明见解析;(2)CF=BC+CD;(3)①CF=CD-BC;②△AOC是等腰三角形.理由见解析.
【解析】试题分析:(1)、①、根据等腰直角的性质得出∠ABC=∠ACB=45°,从而得出四边形ADEF是正方形,根据∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°得出∠BAD=∠CAF,从而得出△BAD和△CAF全等,则∠ACF=∠ABD=45°,从而得出垂直;②、根据 全等得出BD=CF,从而得出结论;(2)、根据(1)的证法的采购员BD=CF,得出CF=BC+CD;(3)、①、根据(1)的证法得出BD=CF,从而得出CF=CD-BC;②、∠BAC=90°,AB=AC得出∠ABD=135°,根据四边形ADEF是正方形得出∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,从而得出△BAD和△CAF全等,则∠ACF=135°,从而得出∠FCD=∠ACF-∠ACB=90°,得出△FCD为直角三角形,根据正方形的性质得出OC=OA,从而说明△FCD为等腰直角三角形.
试题解析:(1)、①、∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, ∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°, ∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°, ∴∠BAD=∠CAF,
在△BAD和△CAF中, AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°, ∴∠ACF+∠ACB=90°, ∴BD⊥CF;
②、由①△BAD≌△CAF可得BD=CF, ∵BD=BC-CD, ∴CF=BC-CD;
(2)、与(1)同理可得BD=CF, 所以,CF=BC+CD;
(3)、①、与(1)同理可得,BD=CF, 所以,CF=CD-BC;
②∵∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, 则∠ABD=180°-45°=135°,
∵四边形ADEF是正方形, ∴AD=AF,∠DAF=90° ∵∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,
∴∠BAD=∠CAF, 在△BAD和△CAF中,AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=180°-45°=135°, ∴∠FCD=∠ACF-∠ACB=90°,则△FCD为直角三角形,
∵正方形ADEF中,O为DF中点, ∴OC=![]() DF ∵在正方形ADEF中,OA=
DF ∵在正方形ADEF中,OA=![]() AEAE=DF, ∴OC=OA,
AEAE=DF, ∴OC=OA,
∴△AOC是等腰三角形

【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量 | 小型汽车数量 | 收取费用 | |
第一天 | 15辆 | 35辆 | 360元 |
第二天 | 18辆 | 20辆 | 300元 |
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?