题目内容
【题目】一个容积为400升的水箱,安装两个有A、B进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
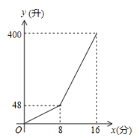
(1)分别求出A、B两注水管的注水速度.
(2)当8≤x≤16时,求y与x之间的函数关系式.
(3)当两水管的注水量相同时,直接写出x的值.
【答案】(1)A水箱注水速度为6升每分,B水箱注水速度为38升每分;
(2)y=44x-304;
(3)x的值为9.6
【解析】试题分析:(1)根据图像,得到注水量为48升,时间为8小时,然后用除法求解,B水箱则先减去A水箱的量,除以时间即可;
(2)根据图像确定两点为(8,48),(16,400),利用待定系数法求解即可;
(3)根据注水速度和时间,列方程可求解.
试题解析:(1)A水箱注水速度为![]() 升/分
升/分
B水箱注水速度为![]() 升/分
升/分
(2)当8=x≤16时设y与x的函数关系为:y=kx+6
则![]()
解得:k=44 , b=-304
∴y=44x-304
(3)x=9.5
当两水箱注水量相同时,x的值为9.5

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目