题目内容
【题目】已知抛物线y1＝x2与直线y2＝－
x＋3相交于A，B两点．
(1)求这两个交点的坐标；
(2)点O的坐标是原点，求△AOB的面积；
(3)直接写出当y1＜y2时，x的取值范围．
【答案】(1) A(－2，4)，B(
，
) ； (2) S△AOB＝
；(3)－2＜x＜.
【解析】
（1）根据解方程组，可得交点坐标；
（2）根据面积的和差，可得答案；
（3）根据函数与不等式的关系，可得答案．
（1）联立抛物线y1=x2与直线y2=-
x+3，得
，
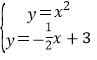解得
，
，
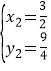A（-2，4），B（，）；
（2）如图，
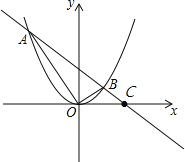
当y=0时，-x+3=0，解得x=6，
即C（6，0）．
S△AOB=S△AOC-S△BOC=×6×4-×6×=；
（3）抛物线在直线的下方，得-2＜x＜．
练习册系列答案
相关题目
【题目】某中学初三年级的同学参加了一项节能的社会调查活动，为了了解家庭用电的情况，他们随即调查了某地50个家庭一年中生活用电的电费支出情况，并绘制了如下不完整的频数分布表和频数分布直方图（费用取整数，单位：元）．
分组/元 | 频 数 | 频 率 |
1000＜x＜1200 | 3 | 0.060 |
1200＜x＜1400 | 12 | 0.240 |
1400＜x＜1600 | 18 | 0.360 |
1600＜x＜1800 | a | 0.200 |
1800＜x＜2000 | 5 | b |
2000＜x＜2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息，解答下列问题：
（1）补全频数分布表a= ，b= ，和频数分布直方图；
（2）这50个家庭电费支出的中位数落在哪个组内？
（3）若该地区有3万个家庭，请你估计该地区有多少个一年电费支出低于1400元的家庭？
