题目内容
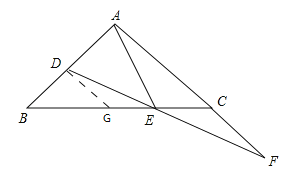
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D.E分别在AB.BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.

(1)求证:DE=EF.
(2)判断BD和CF的数量关系,并说明理由.
【答案】(1)详见解析;(2)BD=CF;详见解析.
【解析】
(1)只要证明EA=ED,EA=EF即可解决问题;
(2)结论:BD=CF.过点D作DG∥AC交BC于G,证明DGE≌FCE ,则DG=CF,再证出DG=BD即可得出结论.
(1)证明:∵∠BAC=90°,
∴∠DAE+∠EAF=90°,
∠ADE+∠F=90°,
∵∠DAE=∠ADE,
∴∠EAF=∠F,
∴EA=EF,
∵∠DAE=∠ADE,
∴EA=ED,
∴DE=EF;
(2)解:BD=CF.
理由:过点D作DG∥AC交BC于G,
∴∠EDG=∠F,
∵ED=EF,∠DEG=∠FEC,
∴DGE≌FCE,
∴DG=CF,
∵AB=AC,
∴∠ACB=∠B,
∵DG∥AC
∴∠ACB=∠DGB,
∴∠B=∠DGB,
∴BD=DG
∴BD=CF.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目