Question

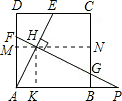
已知：如图，在正方形ABCD中，AD=12，点E是边CD上的动点（点E不与端点C，D重合），AE的垂直平分线FP分别交AD，AE，BC于点F，H，G，交AB的延长线于点P．
（1）设DE=m（0＜m＜12），试用含m的代数式表示

FH

HG

的值；
（2）在（1）的条件下，当

FH

HG

=

1

2

时，求BP的长．

Answer 1

（1）过点H作MN∥AB，分别交AD，BC于M，N两点，
∵FP是线段AE的垂直平分线，
∴AH=EH，
∵MH∥DE，
∴Rt△AHM∽Rt△AED，
∴

AM

MD

=

AH

HE

=1，
∴AM=MD，即点M是AD的中点，
∴AM=MD=6，
∴MH是△ADE的中位线，MH=

1

2

DE=

1

2

m，
∵四边形ABCD是正方形，
∴四边形ABNM是矩形，
∵MN=AD=12，
∴HN=MN-MH=12-

1

2

m，
∵AD∥BC，
∴Rt△FMH∽Rt△GNH，
∴

FH

GH

=

MH

NH

=

1 2 m

12- 1 2 m

，
即

FH

HG

=

m

24-m

（0＜m＜12）；

（2）过点H作HK⊥AB于点K，则四边形AKHM和四边形KBNH都是矩形．
∵

FH

HG

=

m

24-m

=

1

2

，
解得m=8，
∴MH=AK=

1

2

m=

1

2

8=4，HN=KB=12-

1

2

m=12-

1

2

8=8，KH=AM=6，
∵Rt△AKH∽Rt△HKP，
∴

KH

KP

=

AK

HK

，即KH²=AK•KP，
又∵AK=4，KH=6，
∴6²=4•KP，解得KP=9，
∴BP=KP-KB=9-8=1．