题目内容
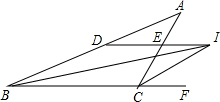
如图，在△AOB中，点C在OA上，点E，D在OB上，且CD∥AB，CE∥AD，AB=AD，试证明△CDE是等腰三角形．
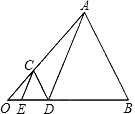
证明：∵CD∥AB，
∴∠CDE=∠B．
又∵CE∥AD，
∴∠CED=∠ADB．
又∵AB=AD，
∴∠B=∠ADB．
∴∠CDE=∠CED．
∴△CDE是等腰三角形．
∴∠CDE=∠B．
又∵CE∥AD，
∴∠CED=∠ADB．
又∵AB=AD，
∴∠B=∠ADB．
∴∠CDE=∠CED．
∴△CDE是等腰三角形．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
