题目内容
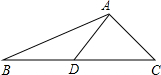
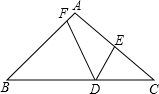
△ABC中,AB=AC=5,BC=6,点D是BC上的一点,那么点D到AB与AC的距离的和为( )
| A.5 | B.6 | C.4 | D.
|
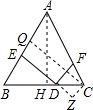
作△ABC的高CQ,AH,过C作CZ⊥DE交ED的延长线于Z,
∵AB=AC=5,BC=6,AH⊥BC,
∴BH=CH=3,
根据勾股定理得:AH=4,
根据三角形的面积公式得:
BC•AH=
AB•CQ,
即:6×4=5CQ,
解得:CQ=
,
∵CQ⊥AB,DE⊥AB,CZ⊥DE,
∴∠CQE=∠QEZ=∠Z=90°,
∴四边形QEZC是矩形,
∴CQ=ZE,
∵∠QEZ=∠Z=90°,
∴∠QEZ+∠Z=180°,
∴CZ∥AB,
∴∠B=∠ZCB,
∵DF⊥AC,CZ⊥DE,
∴∠Z=∠DFC=90°,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACB=∠ZCB,
∵CD=CD,∠ACB=∠ZCB,
∴△ZCD≌△FCD,
∴DF=DZ,
∴DE+DF=CQ=
.
故选D.
∵AB=AC=5,BC=6,AH⊥BC,
∴BH=CH=3,
根据勾股定理得:AH=4,
根据三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
即:6×4=5CQ,
解得:CQ=
| 24 |
| 5 |

∵CQ⊥AB,DE⊥AB,CZ⊥DE,
∴∠CQE=∠QEZ=∠Z=90°,
∴四边形QEZC是矩形,
∴CQ=ZE,
∵∠QEZ=∠Z=90°,
∴∠QEZ+∠Z=180°,
∴CZ∥AB,
∴∠B=∠ZCB,
∵DF⊥AC,CZ⊥DE,
∴∠Z=∠DFC=90°,
∵AB=AC,
∴∠B=∠ACB,
∴∠ACB=∠ZCB,
∵CD=CD,∠ACB=∠ZCB,
∴△ZCD≌△FCD,
∴DF=DZ,
∴DE+DF=CQ=
| 24 |
| 5 |
故选D.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目