题目内容
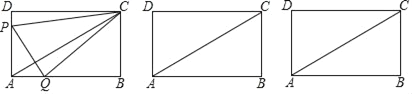
【题目】如图①，在矩形ABCD中，AB=8，AD=4．点P从点A出发，沿A→D→C→D运动，速度为每秒2个单位长度；点Q从点A出发向点B运动，速度为每秒1个单位长度．P、Q两点同时出发，点Q运动到点B时，两点同时停止运动，设点Q的运动时间为t（秒）．连结PQ、AC、CP、CQ．
(1)点P到点C时，t= ；当点Q到终点时，PC的长度为 ；
(2)用含t的代数式表示PD的长；
(3)当三角形CPQ的面积为9时，求t的值．
【答案】(1)6s ；4
；（2）PD=4-2t（0≤t≤2）；PD=2t﹣4（2＜t＜6）；PD=20﹣2t（6≤t≤8）；（3）t=1或t=
.
【解析】
（1）点P到点C时，所走路程为AD+CD=12，点P的速度为每秒2个单位长度；当点Q到终点时，t=8s，据此求解出DP长度并运用勾股定理即可求解PC的长度；
（2）分点P在AD、DC、由C点回头（CD）这三段不同的运动情况进行解答即可；
（3）以上问的结论作为基础，由S△CPQ=S矩形ABCD- S△PAQ- S△PDC- S△CBQ进行解答即可.
解：（1）在矩形ABCD中，AB=8，AD=4
∴CD=AB=8点P到点C时，所走路程为AD+CD=12，
∴t=
=6s
当点Q到终点时，t=8s，P点回到CD中点，
∴DP=4，
由勾股定理得PC=
=4
（2）当0≤t≤2时，PD=4﹣2t
当2＜t＜6时，PD=2t﹣4
当6≤t≤8时，PD=8﹣（2t﹣12）=20﹣2t
（3）当0≤t≤2时，AP=2t，PD=4﹣2t，AQ=t，Q=8﹣t，则，
S△CPQ=4×8﹣
t.2t﹣（8﹣t）.4﹣（4﹣2t ）.8=﹣t2+10t=9，t1=1，t2=9（舍去）
当2＜t＜6时，PC=12﹣2t
S△CPQ=（12﹣2t）4=24﹣4t=9，t=
当6≤t≤8时，PC=2t﹣12
S△CPQ=（2t﹣12）4=4t﹣24=9，t=
（舍去）
综上所述，当三角形CPQ的面积为9时t=1或t=.
