题目内容
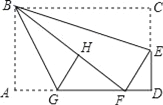
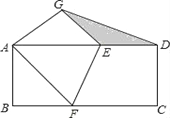
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)DE的长;
(2)求阴影部分△GED的面积.
【答案】(1)3;(2)![]()
【解析】试题分析:(1)设DE=EG=x,则AE=8﹣x.在Rt△AEG中,由勾股定理得:AG2+EG2=AE2,解方程可求出DE的长;
(2)过G点作GM⊥AD于M,根据三角形面积不变性,得到AG×GE=AE×GM,求出GM的长,根据三角形面积公式计算即可.
试题解析:解:(1)设DE=EG=x,则AE=8﹣x.
在Rt△AEG中,AG2+EG2=AE2,∴16+x2=(8﹣x)2,解得x=3,∴DE=3.
(2)过G点作GM⊥AD于M,则![]() AG×GE=
AG×GE=![]() AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,∴GM=
AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,∴GM=![]() ,∴S△GED=
,∴S△GED=![]() GM×DE=
GM×DE=![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4