题目内容
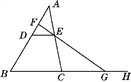
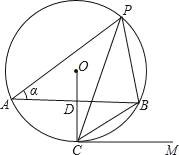
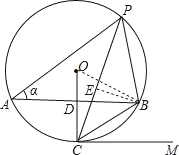
【题目】如图,AB是⊙O的弦,半径OC⊥AB交AB于点D,点P是⊙O上AB上方的一个动点(P不与A、B重合),已知∠APB=60°,∠OCB=2∠BCM.
(1)设∠A=α,当圆心O在∠APB内部时,写出α的取值范围;
(2)求证:CM是⊙O的切线;
(3)若OC=4,PB=4![]() ,求PC的长.
,求PC的长.
【答案】(1)当圆心O在∠APB内时,α的取值范围为30°<α<90°;(2)证明见解析;(3)2![]() +2
+2![]() .
.
【解析】
(1)取特殊情况:当O点在PA上,即AP为直径,根据圆周定理得∠PBA=90°,而∠APB=60°,得到此时∠A=30°;当O点在PB上,即BP为直径,得到∠A=90°;由此得到当圆心O在∠APB内时,α的取值范围为30°<α<90°;
(2)连结OB,根据垂径定理由OC⊥AB得到AC弧=BC弧,再根据圆周角定理得∠APB=∠BCP,于是由∠APB=60°得到∠BPC=30°,然后利用∠BOC=2∠BPC=60°可判断△OBC为等边三角形,则∠MCB=30°,可计算出∠OCM=∠OCB+∠MCB=90°,于是根据切线的判定定理即可得到结论;
(3)作BE⊥PC于E,如图,在Rt△PBE中,根据含30度的直角三角形三边的关系得到BE=![]() PB=2
PB=2![]() ,PE=
,PE=![]() BE=2
BE=2![]() ,再由△OBC为等边三角形得BC=OC=4,则可根据勾股定理计算出CE,然后利用PC=PE+CE进行计算即可.
,再由△OBC为等边三角形得BC=OC=4,则可根据勾股定理计算出CE,然后利用PC=PE+CE进行计算即可.
(1)当O点在PA上,即AP为直径,则∠PBA=90°,而∠APB=60°,所以此时∠A=30°;
当O点在PB上,即BP为直径,则∠A=90°;
所以当圆心O在∠APB内时,α的取值范围为30°<α<90°;
(2)证明:连结OB,如图,
∵OC⊥AB,
∴![]() ,
,
∴∠APB=∠BCP,
∵∠APB=60°,
∴∠BPC=30°,
∴∠BOC=2∠BPC=60°,
∴△OBC为等边三角形,
∴∠OCB=60°,
∵∠OCB=2∠BCM,
∴∠MCB=30°,
∴∠OCM=∠OCB+∠MCB=90°,
∴OC⊥MC,
∴CM与⊙O相切;
(3)作BE⊥PC于E,如图,
在Rt△PBE中,∠BPE=30°,PB=4![]() ,
,
∴BE=![]() PB=2
PB=2![]() ,PE=
,PE=![]() BE=2
BE=2![]() ,
,
∵△OBC为等边三角形,
∴BC=OC=4,
在Rt△BEC中,CE=![]() ,
,
∴PC=PE+CE=![]() .
.