题目内容
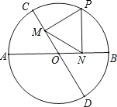
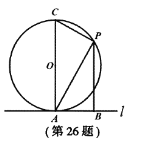
【题目】如图,直线![]() 与⊙
与⊙![]() 相切于点
相切于点![]() 为⊙
为⊙![]() 的直径,
的直径, ![]() 是直径
是直径![]() 右侧半圆上的一个动点(不与点
右侧半圆上的一个动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 、
、![]() .设
.设![]() ,
, ![]() .求: (1)
.求: (1)![]() 与
与![]() 相似吗?为什么?
相似吗?为什么?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 取得最大值,最大值为多少?
取得最大值,最大值为多少?
【答案】(1)详见解析;(2)![]() ;(3)2.
;(3)2.
【解析】
(1)利用切线的性质以及平行线的性质进而得出∠CAP=∠APB以及∠PBA=∠APC=90°,即可得出答案;
(2)根据相似三角形的性质即可得到结论;
(3)由![]() x2代替y,化为关于x的二次三项式,配方即可求得答案.
x2代替y,化为关于x的二次三项式,配方即可求得答案.
解:(1)△APC∽△APB,
证明:∵⊙O与直线l相切于点A,且AB为⊙O的直径,
∴CA⊥l,∠CPA=90°,
又∵PB⊥l,
∴CA∥PB,
∴∠CAP=∠APB,
又∵PB⊥l,
∴∠APB=90°,
∴∠CAP=∠ABP,
∴△APC∽△APB;
(2)∵△APC∽△APB,
∴![]() ,
,
∴ ![]() .
.
∴ ![]() (0<x<8);
(0<x<8);
(3)x-y=x-![]() =-
=-![]() (x-4)2+2,
(x-4)2+2,
∴当x为4时,x-y取得最大值,最大值为2.

练习册系列答案
相关题目
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4