题目内容
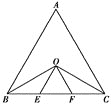
【题目】如图所示，在△ABC中，AD⊥BC于点D，AE为∠BAC的平分线，且∠DAE＝15°，∠B＝35°，则∠C＝________°.
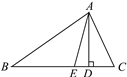
【答案】65
【解析】
由∠DAE=15°，∠ADE=90°，根据直角三角形两锐角互余可得∠AED=90°-∠DAE=75°，再根据三角形外角的性质可得∠BAE=∠AED-∠B=40°，再根据角平分线的定义求得∠BAC=2∠BAE=80°，再由三角形内角和定理即可求得∠C的度数.
∵∠DAE=15°，∠ADE=90°，
∴∠AED=90°-∠DAE=75°，
∴∠BAE=∠AED-∠B=75°-35°=40°，
∵AE平分∠BAC，
∴∠BAC=2∠BAE=80°，
∴∠C=180°-∠B-∠BAC=65°，
故答案为：65.
练习册系列答案
相关题目
【题目】列方程解应用题：五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 20 | 30 |
售价（元/件） | 29 | 40 |
（1）新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该购物中心第二次以第一次的进价又购进甲、乙两种商品，其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元，求第二次乙种商品是按原价打几折销售？
