题目内容
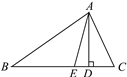
【题目】如图,△ABC为等边三角形,∠ABC、∠ACB的平分线相交于点O,OE∥AB交BC于点E,OF∥AC交BC于点F,图中等腰三角形共有( )
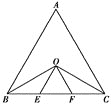
A. 6个 B. 5个 C. 4个 D. 3个
【答案】B
【解析】
由已知条件,首先得到∠OBC=∠OCB,利用两个角相等即为等腰三角形,得到△BOC为等腰三角形;然后在题中找出对应角相等即可.
解:∵△ABC为正三角形,∴△ABC为等腰三角形;
∵OB,OC为角平分线,∴∠OBC=∠OCB,∴△BOC为等腰三角形;
∵OE∥AB,∴∠ABO=∠BOE=∠OBE,∴△BOE为等腰三角形;
同理,△COF为等腰三角形;
∠OEF=∠OFE,∴△EOF为等腰三角形.
所以题中共有5个等腰三角形
故选:B.

练习册系列答案
相关题目