题目内容
【题目】综合题
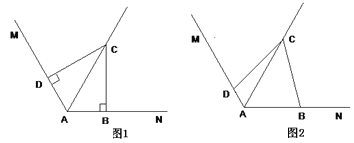
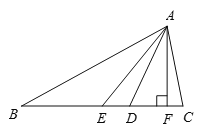
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.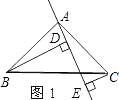
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.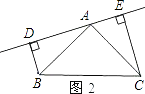
【答案】
(1)解:∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵  ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE=AD+DE,
∴BD=DE+CE;
(2)解:BD=DE﹣CE;
∵∠BAC=90°,BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,
∴∠ABD+∠DAB=∠DAB+∠CAE,
∴∠ABD=∠CAE,
∵AB=AC,
在△ABD和△CAE中,
∵  ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴AD+AE=BD+CE,
∵DE=BD+CE,
∴BD=DE﹣CE.
【解析】(1)根据三角形内角和定理求出∠ABD=∠CAE,根据三角形全等的条件得到△ABD≌△CAE,得到全等三角形的对应边、对应角相等,证明得到BD=DE+CE;(2)根据旋转的性质,得到∠ABD=∠CAE,得到△ABD≌△CAE,到全等三角形的对应边、对应角相等,证明得到BD=DE-CE.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.

 应用题作业本系列答案
应用题作业本系列答案【题目】研究发现,地表以下岩层的温度与它所处的深度有表中所示的关系:
岩层的深度 | 1 | 2 | 3 | 4 | 5 | 6 | … |
岩层的温度 | 55 | 90 | 125 | 160 | 195 | 230 | … |
根据以上信息,回答下列问题:
(1)上表反映的两个变量之中,________是自变量,_______是因变量;
(2)岩层的深度![]() 每增加
每增加![]() ,温度
,温度![]() 是怎样变化的?试写出
是怎样变化的?试写出![]() 和
和![]() 的关系式;
的关系式;
(3)估计岩层![]() 深处的温度是多少?
深处的温度是多少?