题目内容
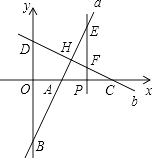
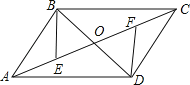
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF.
(1) 求证:△BOE≌△DOF;
(2) 连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
【答案】(1)见解析;(2)四边形EBDF为菱形,理由见解析
【解析】
(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;
(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
证明:(1) ∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中
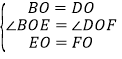 ,
,
∴△BOE≌△DOF(SAS);
(2) 四边形EBDF为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?