题目内容
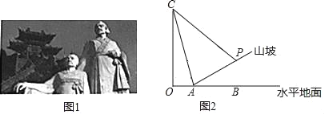
【题目】某游客计划测量这座塑像的高度,(如图1),由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7,![]() ,
,![]() ,
,![]() )
)
【答案】塑像的高度约为 17.5 米.
【解析】
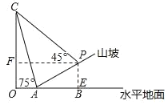
过点P作PE⊥OB于点E,PF⊥OC于点F,设PE=x,则AE=3x,在Rt△AEP中根据勾股定理得PE,在Rt△AOC中,由tan75°求得m的值,继而可得答案.
过点 P 作 PE⊥OB 交 OB 于点 E,PF⊥OC 交 OC 于点 F,
∵i=1:3,AP=10,
设 PE=x,则 AE=3x,
在 Rt△AEP 中,x2+(3x)2=102,
解得:![]() 或
或![]() (舍),
(舍),
∴![]() ,则
,则![]() ,
,
∵∠CPF=∠PCF=45°,
∴CF=PF,
设 CF=PF=m 米,则![]() 米,
米,![]() 米,
米,
在 Rt△AOC 中,![]() 即
即![]()
解得:m≈14.3,
∴![]() 米,
米,
答:塑像的高度约为 17.5 米.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目