题目内容
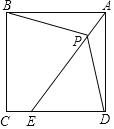
【题目】如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=6,则图中阴影部分的面积为( )
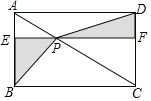
A.10B.12C.16D.18
【答案】B
【解析】
由矩形的性质可证明S△PEB=S△PFD,即可求解.
作PM⊥AD于M,交BC于N.
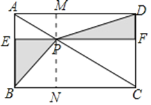
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴s矩形PEBN=S矩形PMDF
∵S△PBE=![]() S矩形PEBN,S△PFD=
S矩形PEBN,S△PFD=![]() S矩形PMDF,
S矩形PMDF,
∴S△DFP=S△PBE
∵MP=AE=2
∴S△DFP=S△PBE=![]() ×2×6=6,
×2×6=6,
∴S阴=6+6=12,
故选:B.

练习册系列答案
相关题目
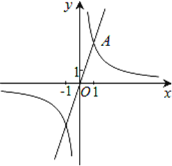
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x的图象与反比例函数![]() 的图象的一个交点为A(1,m).
的图象的一个交点为A(1,m).
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若点P在直线OA上,且满足PA=2OA,直接写出点P的坐标.