题目内容
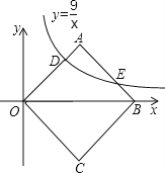
【题目】已知反比例函数![]() 与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时这两个函数值相等.
与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时这两个函数值相等.
(1)求这两个函数的解析式;
(2)直接写出当x取何值时,![]() 成立.
成立.
【答案】(1)一次函数的解析式为![]() ;反比例函数解析式为
;反比例函数解析式为![]() ;(2)x<-2或0<x<3
;(2)x<-2或0<x<3
【解析】
(1)先把点(-2,-1)代入y=![]() ,求出反比例函数解析式;再把x=3代入求出y的值,把点(-2,-1)和x=3时y的值代入一次函数解析式即可求出一次函数的解析式;
,求出反比例函数解析式;再把x=3代入求出y的值,把点(-2,-1)和x=3时y的值代入一次函数解析式即可求出一次函数的解析式;
(2)找出反比例函数在一次函数图象上方对应的自变量的取值范围即可.
解:∵反比例函数y=![]() 的图象经过(-2,-1),
的图象经过(-2,-1),
∴-1=![]() ,即m=2,
,即m=2,
∴反比例函数解析式为y=![]() ;
;
当x=3时,y=![]() .
.
把(-2,-1)、(3,![]() )代入y=kx+b,
)代入y=kx+b,
得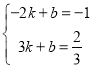 ,
,
解得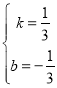 ,
,
∴一次函数的解析式为y=![]() x-
x-![]() ;
;
(2)∵反比例函数y=![]() 与一次函数y=kx+b的图象交于点(-2,-1)、(3,
与一次函数y=kx+b的图象交于点(-2,-1)、(3,![]() ),
),
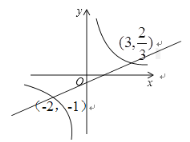
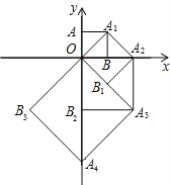
由图象可知:当x<-2或0<x<3时,反比例函数在一次函数图象的上方,
∴当x<-2或0<x<3时,![]() >kx+b成立.
>kx+b成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?