题目内容
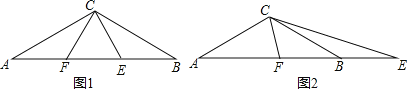
【题目】如图1,△ABC中,CA=CB,∠ACB=120°,AB=3,点E、F在直线AB上,且∠ECF=60°.
(1)求AC边的长;
(2)如图1,点E、F在线段AB上时,若EF=AF,求证:BE=EF;
(3)如图2,F在AB上,E在AB的延长线上时,AF=m,BE=n,则n= (用含m的式子表示).
【答案】(1)AC=![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)过点C作CD⊥AB于点D,由直角三角形的性质可得AB=2![]() CD,AC=2CD,即可求AC的值;
CD,AC=2CD,即可求AC的值;
(2)作点A关于直线CF的对称点G,连接FG、CG、EG,由“SAS”可证△GCE≌△BCE,可得EG=BE,∠B=∠EGC,即可证△FEG为等边三角形,可得结论;
(2)将△BCE绕点C顺时针旋转60°,得到△GCH,连接AG,过点H作DH⊥CG,由旋转的性质可得BC=CG,BE=GH=n,∠BCG=60°,∠CGH=∠CBE=180°﹣∠ACB=150°,通过证明△NCF∽△DCH,可得![]() ,即可求解.
,即可求解.
(1)如图1,过点C作CD⊥AB于点D,
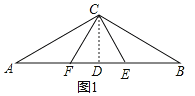
∵CA=CB,∠ACB=120°,
∴∠A=∠B=30°,AD=BD
∴AC=2CD,BD=AD=![]() CD,
CD,
∵AB=3,
∴AD+BD=AB=3=2![]() CD
CD
∴CD=![]()
∴AC=![]()
(2)如图1﹣1,作点A关于直线CF的对称点G,连接FG、CG、EG,

∵G为点A关于直线CF的对称点;
∴△ACF≌△GCF,
∴AC=CG,∠ACF=∠GCF,∠FGC=∠A.
又∵AC=BC,
∴CG=CB,
∵∠ACB=120°,∠ECF=60°,
∴∠ECG=60°﹣∠GCF=60°﹣∠ACF,∠BCE=60°﹣∠ACF,
∴∠ECG=∠ECB,
在△GCE和△BCE中
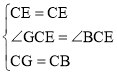
∴△GCE≌△BCE(SAS),
∴EG=BE,∠B=∠EGC,
∵∠ACB=120°,
∴∠A+∠B=60°,
∴∠EGC+∠FGC=60°,
又∵AF=EF=FG,
∴△FEG为等边三角形,
∴EF=EG=BE,即BE=EF.
(2)如图2,将△BCE绕点C顺时针旋转60°,得到△GCH,连接AG,过点H作DH⊥CG,
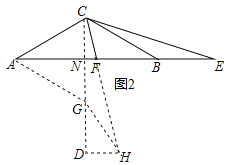
∵将△BCE绕点C顺时针旋转60°,得到△GCH,
∴BC=CG,BE=GH=n,∠BCG=60°,∠CGH=∠CBE=180°﹣∠ACB=150°
∴∠DGH=180°﹣∠CGH=30°,且DH⊥CG
∴DH=![]() GH=
GH=![]() ,GD=
,GD=![]() DH=
DH=![]() n,
n,
∵∠ACB=120°,∠BCG=60°
∴∠ACG=∠BCG=60°,且AC=BC
∴CG⊥AB,AN=BN=![]() ,CN=
,CN=![]()
∴FN=m﹣![]()
∵∠CNF=∠CDH=90°,∠NCF=∠DCH,
∴△NCF∽△DCH
∴![]()
∴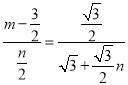
∴n=![]()
故答案为:![]()

 阅读快车系列答案
阅读快车系列答案