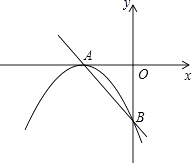Question

【题目】在平面直角坐标系xOy中，抛物线y=ax2+2ax﹣3a（a＞0）与x轴交于A，B两点（点A在点B的左侧）．
（1）求抛物线的对称轴及线段AB的长；
（2）抛物线的顶点为P，若∠APB=120°，求顶点P的坐标及a的值；
（3）若在抛物线上存在一点N，使得∠ANB=90°，结合图象，求a的取值范围．

Answer 1

【答案】
（1）

解：令y=0得：ax2+2ax﹣3a=0，即a（x+3）（x﹣1）=0，解得：x=﹣3或x=1，

∴A（﹣3，0）、B（1，0）．

∴抛物线的对称轴为直线x=﹣1，AB=4

（2）

解：如图1所示：

设抛物线的对称轴与x轴交于点H．

∵∠APB=120°，AB=4，PH在对称轴上，

∴AH=2，∠APB=60°．

∴PH= ．

∴点P的坐标为（﹣1，﹣ ）．

将点P的坐标代入得：﹣ =﹣4a，解得a=

（3）

解：如图2所示：以AB为直径作⊙H．

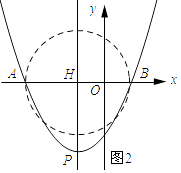
∵当∠ANB=90°，

∴点N在⊙H上．

∵点N在抛物线上，

∴点N为抛物线与⊙H的交点．

∴点P在圆上或点P在圆外．

∴HP≥2．

∵将x=﹣1代入得：y=﹣4a．

∴HP=4a．

∴4a≥2，解得a≥ ．

∴a的取值范围是a≥

【解析】（1）令y=0得：ax2+2ax﹣3a=0，解关于x的方程可求得点A和点B的横坐标，然后可求得AB的长，利用抛物线的对称性可得到抛物线的对称轴方程；（2）如图1所示，利用抛物线的对称性可知：AH=2，∠APB=60°，然后可求得PH= ，从而可的点P的坐标，最后将点P的坐标代入抛物线的解析式可求得a的值；（3）以AB为直径作⊙H，则点N在⊙H上，当点P在⊙H上或点P在⊙H外时，∠ANB=90°，故此HP≥2，接下来，依据HP≥2列不等式求解即可．
【考点精析】本题主要考查了二次函数的性质和抛物线与坐标轴的交点的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．