题目内容
【题目】如图,在平面直角坐标系中,顶点为(3,4)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有什么位置关系,并给出证明;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线解析式为:y=a(x﹣3)2+4,
将A(0,﹣5)代入求得:a=﹣1,
∴抛物线解析式为y=﹣(x﹣3)2+4=﹣x2+6x﹣5
(2)
解:抛物线的对称轴l与⊙C相离.证明:
令y=0,即﹣x2+6x﹣5=0,得x=1或x=5,
∴B(1,0),C(5,0).
如答图①所示,
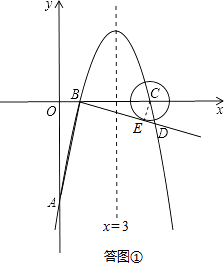
设切点为E,连接CE,
由题意易证Rt△ABO∽Rt△BCE,
∴ ![]() ,
,
即 ![]() ,
,
求得⊙C的半径CE= ![]() =
= ![]() =
= ![]() ;
;
而点C到对称轴x=3的距离为2,2> ![]() ,
,
∴抛物线的对称轴l与⊙C相离
(3)
解:存在.理由如下:
有两种情况:
(i)如答图②所示,
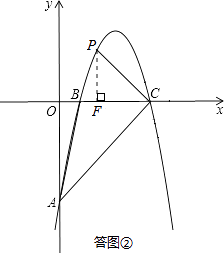
点P在x轴上方.
∵A(0,﹣5),C(5,0),
∴△AOC为等腰直角三角形,∠OCA=45°;
∵PC⊥AC,∴∠PCO=45°.
过点P作PF⊥x轴于点F,则△PCF为等腰直角三角形.
设点P坐标为(m,n),则有OF=m,PF=CF=n,
OC=OF+CF=m+n=5 ①
又点P在抛物线上,
∴n=﹣m2+6m﹣5 ②
联立①②式,解得:m=2或m=5.
当m=5时,点P与点C重合,故舍去,
∴m=2,
∴n=3,
∴点P坐标为(2,3);
(ii)如答图③所示,
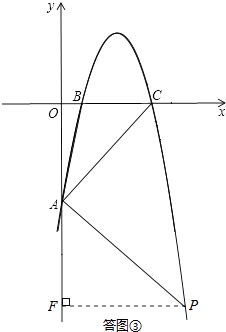
点P在x轴下方.
∵A(0,﹣5),C(5,0),
∴△AOC为等腰直角三角形,∠OAC=45°;
过点P作PF⊥y轴于点F,
∵PA⊥AC,
∴∠PAF=45°,即△PAF为等腰直角三角形.
设点P坐标为(m,n),则有PF=AF=m,OF=﹣n=OA+AF=5+m,
∴m+n=﹣5 ①
又点P在抛物线上,
∴n=﹣m2+6m﹣5 ②
联立①②式,解得:m=0或m=7.
当m=0时,点P与原点重合,故舍去,
∴m=7,
∴n=﹣12,
∴点P坐标为(7,﹣12).
综上所述,存在点P,使△ACP是以AC为直角边的直角三角形.点P的坐标为(2,3)或(7,﹣12).
【解析】(1)由顶点式,利用待定系数法求出抛物线的解析式;(2)判断直线与圆的位置关系,关键是分析圆的半径r和圆心到直线距离d之间的大小关系.由题意可知d=2,由相似三角形求得r= ![]() ,因为2>
,因为2> ![]() ,所以可判定抛物线的对称轴l与⊙C相离;(3)本问是存在性问题.点P有两种情况,分别位于x轴上方与下方,需要分类讨论,注意不要漏解;在求点P坐标时,需要充分利用几何图形(等腰直角三角形)的性质,以及抛物线上点的坐标特征.
,所以可判定抛物线的对称轴l与⊙C相离;(3)本问是存在性问题.点P有两种情况,分别位于x轴上方与下方,需要分类讨论,注意不要漏解;在求点P坐标时,需要充分利用几何图形(等腰直角三角形)的性质,以及抛物线上点的坐标特征.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).