题目内容
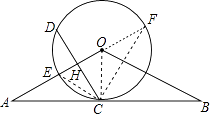
【题目】如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB,OA交⊙O于点E. 
(1)证明:直线AB与⊙O相切;
(2)若AE=a,AB=b,求⊙O的半径;(结果用a,b表示)
(3)过点C作弦CD⊥OA于点H,试探究⊙O的直径与OH、OB之间的数量关系,并加以证明.
【答案】
(1)证明:如图所示:连接CO,
∵OA=OB,AC=BC,
∴OC⊥AB,
∵OC为⊙O的半径,
∴直线AB与⊙O相切
(2)解:在直角三角形OAC中用勾股定理就可以了.设半径为r,则OC=r,OA=a+r,
AC= ![]() AB=
AB= ![]() b,
b,
在Rt△AOC中,
OC2+AC2=OA2,
则r2+ ![]() b2=(a+r)2,
b2=(a+r)2,
解得:r= ![]() ﹣
﹣ ![]()
(3)解:d2=4OH×OB,
理由:∵OA⊥CD,OC⊥AC,
∴∠OCA=∠OHC,
∵∠HOC=∠COA,
∴△HOC∽△COA,
∴ ![]() ,
,
即OC2=OH×OA,
∵OC垂直平分AB,
∴OA=OB,
设直径为d,则OC= ![]() ,
,
∴( ![]() )2=OH×OB,
)2=OH×OB,
即d2=4OH×OB.
【解析】(1)利用段垂直平分线的性质得出OC⊥AB,进而得出答案即可;(2)利用勾股定理得出OC2+AC2=OA2 , 进而得出⊙O的半径;(3)首先得出△HOC∽△COA,进而得出OC2=OH×OA,即可得出⊙O的直径与OH、OB之间的数量关系.

练习册系列答案
相关题目