题目内容
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
【答案】
(1)解:令y=0,则﹣x2+3x+4=0,
即(x+1)(x﹣4)=0.
解得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0),
令x=0,得y=4,所以C(0,4),
当x=3时,y=﹣32+3×3+4=4,
所以D(3,4)。
(2)解:∵OC=OB=4,
∴∠ABC=45°,
∵C、D的纵坐标相同,
∴CD∥AB.
又∵OC=OB,
∴∠BCD=∠OBC=45°
(3)解:过点D作DE⊥BC于点E, 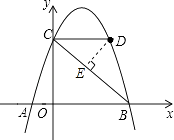
在Rt△OBC中,得BC=4 ![]() ,
,
在Rt△CDE中,∵CD=3,
∴CE=ED= ![]()
![]() ,
,
∴BE=BC﹣CE= ![]()
![]() ,
,
∴tan∠DBC= ![]() =
= ![]() .
.
【解析】(1)将y=0和x=0,x=3分别代入函数解析式,求出对应的自变量的值和对应的函数值,即可求出A、B、C、D的坐标。
(2)根据点B的横坐标和点C的纵坐标相等,即可证出△OBC是等腰直角三角形,得出∠ABC=45°,再观察点C、点D的纵坐标相等得出CD∥AB,根据平行线的性质即可求出结果。
(3)添加辅助线将∠DBC转化到直角三角形中,因此过点D作DE⊥BC于点E,先根据点C和点D的坐标求出CD的长,在Rt△OBC中和在Rt△CDE中分别求出BC、DE的长,就可以求出BE的长,从而求得结果。
【考点精析】掌握抛物线与坐标轴的交点和勾股定理的概念是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 阅读快车系列答案
阅读快车系列答案