题目内容
【题目】如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 . 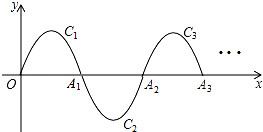
【答案】2
【解析】解:∵一段抛物线:y=﹣x(x﹣3)(0≤x≤3),
∴图象与x轴交点坐标为:(0,0),(3,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.
∴C13的解析式与x轴的交点坐标为(36,0),(39,0),且图象在x轴上方,
∴C13的解析式为:y13=﹣(x﹣36)(x﹣39),
当x=37时,y=﹣(37﹣36)×(37﹣39)=2.
所以答案是:2.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.

练习册系列答案
相关题目
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术字画 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= , b=;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?