题目内容
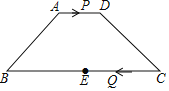
【题目】如图，在ABCD中，AE⊥BD，CF⊥BD，E，F分别为垂足．
（1）求证：四边形AECF是平行四边形；
（2）如果AE=3，EF=4，求AF、EC所在直线的距离．
【答案】(1)证明见解析；(2) AF、EC所在直线的距离是2.4.
【解析】
(1) 先证△ADE≌△CBF，据此得出AD=BC，结合AD∥BC即可得证．
（2）根据勾股定理和三角形面积的不同计算方法即可解答.
(1)∵AE⊥BD，CF⊥BD，∴∠AED=∠CFB=90°，∴AE∥CF，在ABCD中，∵AD∥BC，∴∠ADE＝∠CBF，又∵AD＝CB，∴△ADE≌△CBF(AAS)，∴AE＝CF，∴四边形AECF是平行四边形(其他证法参照给分)；
(2)在AECF中，AF∥EC，设AF、EC所在直线的距离为h.∵AE⊥BD，∴∠AEF=90°，∴AF=
=5，∵SAECF=AE·EF=AF·h，∴h=
=2.4,∴AF、EC所在直线的距离是2.4.
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
