ЬтФПФкШн
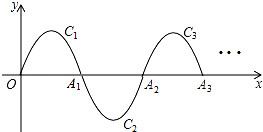
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bx+4ОЙ§AЃЈЉ3ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌЧвгыyжсНЛгкЕуCЃЌЕуDдкxжсЕФИКАыжсЩЯЃЌЧвBD=BCЃЌгавЛЖЏЕуPДгЕуAГіЗЂЃЌбиЯпЖЮABвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуBвЦЖЏЃЌЭЌЪБСэвЛИіЖЏЕуQДгЕуCГіЗЂЃЌбиЯпЖЮCAвдФГвЛЫйЖШЯђЕуAвЦЖЏЃЎ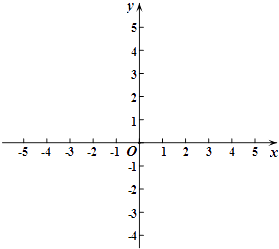
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєОЙ§tУыЕФвЦЖЏЃЌЯпЖЮPQБЛCDДЙжБЦНЗжЃЌЧѓДЫЪБtЕФжЕЃЛ
ЃЈ3ЃЉИУХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуMЃЌЪЙMQ+MAЕФжЕзюаЁЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЁпХзЮяЯпy=ax2+bx+4ОЙ§AЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌ
Ёр ![]() ЃЌНтЕУ
ЃЌНтЕУ 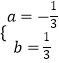 ЃЌ
ЃЌ
ЁрЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љ ![]() x2+
x2+ ![]() x+4
x+4
ЃЈ2ЃЉНтЃКШчЭМ1ЃЌвРЬтвтжЊAP=tЃЌСЌНгDQЃЌ
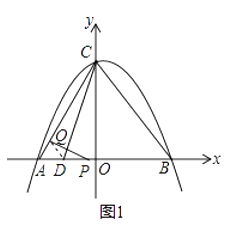
ЁпAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЌ
ЁрAC=5ЃЌBC=4 ![]() ЃЌAB=7ЃЎ
ЃЌAB=7ЃЎ
ЁпBD=BCЃЌ
ЁрAD=ABЉBD=7Љ4 ![]() ЃЌ
ЃЌ
ЁпCDДЙжБЦНЗжPQЃЌ
ЁрQD=DPЃЌЁЯCDQ=ЁЯCDPЃЎ
ЁпBD=BCЃЌ
ЁрЁЯDCB=ЁЯCDBЃЎ
ЁрЁЯCDQ=ЁЯDCBЃЎ
ЁрDQЁЮBCЃЎ
ЁрЁїADQЁзЁїABCЃЎ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
НтЕУDP=4 ![]() Љ
Љ ![]() ЃЌ
ЃЌ
ЁрAP=AD+DP= ![]() ЃЎ
ЃЎ
ЁрЯпЖЮPQБЛCDДЙжБЦНЗжЪБЃЌtЕФжЕЮЊ ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉНтЃКШчЭМ2ЃЌЩшХзЮяЯпy=Љ ![]() x2+
x2+ ![]() x+4ЕФЖдГЦжсx=
x+4ЕФЖдГЦжсx= ![]() гыxжсНЛгкЕуEЃЎЕуAЃЌBЙигкЖдГЦжсx=
гыxжсНЛгкЕуEЃЎЕуAЃЌBЙигкЖдГЦжсx= ![]() ЖдГЦЃЌСЌНгBQНЛИУЖдГЦжсгкЕуMЃЎ
ЖдГЦЃЌСЌНгBQНЛИУЖдГЦжсгкЕуMЃЎ
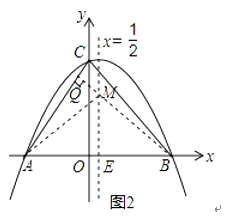
дђMQ+MA=MQ+MBЃЌМДMQ+MA=BQЃЌ
ЁпЕБBQЁЭACЪБЃЌBQзюаЁЃЌДЫЪБЃЌЁЯEBM=ЁЯACOЃЌ
ЁрtanЁЯEBM=tanЁЯACO= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌНтME=
ЃЌНтME= ![]() ЃЎ
ЃЎ
ЁрMЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌМДдкХзЮяЯпy=Љ
ЃЉЃЌМДдкХзЮяЯпy=Љ ![]() x2+
x2+ ![]() x+4ЕФЖдГЦжсЩЯДцдквЛЕуMЃЈ
x+4ЕФЖдГЦжсЩЯДцдквЛЕуMЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЪЙЕУMQ+MAЕФжЕзюаЁ
ЃЉЃЌЪЙЕУMQ+MAЕФжЕзюаЁ
ЁОНтЮіЁПЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЃЌАбAЁЂBзјБъДњШыНтЮіЪНЃЌЕУЕНЗНГЬзщЃЌЧѓГіaЁЂbМДПЩЃЛЃЈ2ЃЉгЩДЙжБЦНЗжЯпаджЪКЭвбжЊЬѕМўПЩЕУГіЁїADQЁзЁїABCЃЌЖдгІБпГЩБШР§ЃЌЧѓГіDPЃЌНјЖјЧѓГіAP=AD+DPЃЌМДПЩЧѓГіЪБМфt;ЃЈ2ЃЉвЊЧѓMQ+MAЕФжЕзюаЁЃЌПЩВЩгУЖдГЦЗЈЃЌMQ+MAПЩзЊЛЏЮЊMQ+MBЃЌMQ+MA=BQЃЌМДЧѓBQЕФзюаЁжЕЃЌЕБBQЁЭACЪБЃЌBQзюаЁЃЌПЩРћгУtanЁЯEBM=tanЁЯACO= ![]() ,СаГіЕШЪНЃЌЧѓГіMзнзјБъ.
,СаГіЕШЪНЃЌЧѓГіMзнзјБъ.

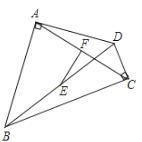
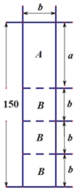
ЁОЬтФПЁПзАЪЮЙЋЫОЮЊаЁУїМвЩшМЦЕчЪгБГОАЧНЪБашвЊAЁЂBаЭАхВФШєИЩПщЃЌAаЭАхВФЙцИёЪЧabЃЌBаЭАхВФЙцИёЪЧbbЃЎЯжжЛФмЙКЕУЙцИёЪЧ150bЕФБъзМАхВФЃЎЃЈЕЅЮЛЃКcmЃЉ
ЃЈ1ЃЉШєЩшa60cmЃЌb30cmЃЎвЛеХБъзМАхВФОЁПЩФмЖрЕФВУГіAаЭЁЂBаЭАхВФЃЌЙВгаЯТБэШ§жжВУЗЈЃЌЯТЭМЪЧВУЗЈвЛЕФВУМєЪОвтЭМЃЎ
ВУЗЈвЛ | ВУЗЈЖў | ВУЗЈШ§ | |
AаЭАхВФПщЪ§ | 1 | 2 | 0 |
BаЭАхВФПщЪ§ | 3 | m | n |
дђЩЯБэжаЃЌ m=___________ЃЌ n=__________ЃЛ
ЃЈ2ЃЉЮЊСЫзАаоЕФашвЊЃЌаЁУїМвгжЙКТђСЫШєИЩCаЭАхВФЃЌЦфЙцИёЪЧaaЃЌВЂзіГЩШчЯТЭМЕФБГОАЧНЃЎЧыаДГіЯТЭМжаЫљБэЪОЕФЕШЪНЃК__________ЃЛ
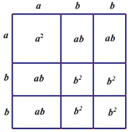
(3)ШєИјЖЈвЛИіЖўДЮШ§ЯюЪН2a25ab3b2ЃЌЪдгУЦДЭМЕФЗНЪННЋЦфвђЪНЗжНтЃЎЃЈЧыЗТееЃЈ2ЃЉдкМИКЮЭМаЮжаБъЩЯгаЙиЪ§СПЃЉ
ЁОЬтФПЁПАзЩЋЮлШОЃЈ WhitepollutionЃЉЪЧШЫУЧЖдФбНЕНтЕФЫмСЯРЌЛјЃЈЖржИЫмСЯДќЃЉЮлШОЛЗОГЯжЯѓЕФвЛжжаЮЯѓГЦЮНЃЎЮЊСЫШУШЋаЃЭЌбЇИаЪмЖЊЦњЫмСЯДќЖдЛЗОГЕФгАЯьЃЌаЁБђЫцЛњГщШЁФГаЁЧј![]() ЛЇОгУёЃЌМЧТМСЫетаЉМвЭЅ
ЛЇОгУёЃЌМЧТМСЫетаЉМвЭЅ![]() ФъФГИідТЖЊЦњЫмСЯДќЕФЪ§СПЃЈЕЅЮЛЃКИіЃЉ
ФъФГИідТЖЊЦњЫмСЯДќЕФЪ§СПЃЈЕЅЮЛЃКИіЃЉ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЧыИљОнЩЯЪіЪ§ОнЃЌНтД№вдЯТЮЪЬтЃК

ЃЈ1ЃЉаЁБђАДЁАзщОрЮЊ![]() ЁБСаГіСЫШчЯТЕФЦЕЪ§ЗжВМБэЃЈУПзщЪ§ОнКЌзюаЁжЕВЛКЌзюДѓжЕЃЉЃЌЧыНЋБэжаПеШБЕФВПЗжВЙГфЭъећЃЌВЂВЙШЋЦЕЪ§жБЗНЭМЃЛ
ЁБСаГіСЫШчЯТЕФЦЕЪ§ЗжВМБэЃЈУПзщЪ§ОнКЌзюаЁжЕВЛКЌзюДѓжЕЃЉЃЌЧыНЋБэжаПеШБЕФВПЗжВЙГфЭъећЃЌВЂВЙШЋЦЕЪ§жБЗНЭМЃЛ
Зжзщ | ЛЎМЧ | ЦЕЪ§ |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
КЯМЦ | / |
|
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЕФжБЗНЭМПЩвдПДГіЃЌет![]() ЛЇОгУёМветИідТЖЊЦњЫмСЯДќЕФИіЪ§дк зщЕФМвЭЅзюЖрЃЛЃЈЬюЗжзщађКХЃЉ
ЛЇОгУёМветИідТЖЊЦњЫмСЯДќЕФИіЪ§дк зщЕФМвЭЅзюЖрЃЛЃЈЬюЗжзщађКХЃЉ
ЃЈ3ЃЉИљОнЦЕЪ§ЗжВМБэЃЌаЁБђгжЛГіСЫШчЭМЫљЪОЕФЩШаЮЭГМЦЭМЃЎЧыНЋЭГМЦЭМжаИїзщеМзмЪ§ЕФАйЗжБШЬюдкЭМжаЃЌВЂЧѓГі![]() зщЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
зщЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉШєИУаЁЧјЙВга![]() ЛЇОгУёМвЭЅЃЌЧыФуЙРМЦУПдТЖЊЦњЕФЫмСЯДќЪ§СПВЛаЁгк
ЛЇОгУёМвЭЅЃЌЧыФуЙРМЦУПдТЖЊЦњЕФЫмСЯДќЪ§СПВЛаЁгк![]() ИіЕФМвЭЅИіЪ§ЃЎ
ИіЕФМвЭЅИіЪ§ЃЎ