Question

【题目】如图，抛物线y= x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．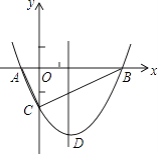

（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．

Answer 1

【答案】
（1）解：∵点A（﹣1，0）在抛物线y= x2+bx﹣2上，

∴ ×（﹣1 ）2+b×（﹣1）﹣2=0，

解得：b=﹣ ，

∴抛物线的解析式为y= x2﹣ x﹣2．

y= （x﹣ ）2﹣ ，

∴顶点D的坐标为：（ ，﹣ ）

（2）解：当x=0时y=﹣2，∴C（0，﹣2），OC=2．

当y=0时， x2﹣ x﹣2=0，

解得：x1=﹣1，x2=4，

∴B （4，0），

∴OA=1，OB=4，AB=5．

∵AB2=25，AC2=OA2+OC2=5，BC2=OC2+OB2=20，

∴AC2+BC2=AB2．

∴△ABC是直角三角形．

（3）解：如图所示：连接AM，

点A关于对称轴的对称点B，BC交对称轴于点M，根据轴对称性及两点之间线段最短可知，

MC+MA的值最小，即△ACM周长最小，

设直线BC解析式为：y=kx+d，则 ，

解得： ，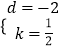

故直线BC的解析式为：y= x﹣2，

当x= 时，y=﹣ ，

∴M（ ，﹣ ），

△ACM最小周长是：AC+AM+MC=AC+BC= +2 =3 ．

【解析】（1）将点A的坐标代入抛物线的解析式即可求出b的值；再将二次函数配方成顶点式，即可写出顶点坐标。
（2）先求出抛物线与x轴、y轴的交点坐标，即求出当x=0时y的值和y=0时x的值，再利用勾股定理求出AB2，AC2，BC2，再比较AC2+BC2与AB2的大小即可判断。
（3）抓住已知条件点M是抛物线对称轴上的一个动点且当△ACM周长最小，可知点A和点B关于抛物线的对称轴对称，因此连接BC交对称轴于点M，连接AM，先求出直线BC的函数解析式，再根据抛物线的顶点坐标即可求出点,M的坐标，然后利用勾股定理求出BC、AC的长，△ACM的最小周长=BC+AC，即可求出结果。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对抛物线与坐标轴的交点的理解，了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．