题目内容
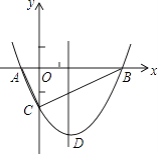
【题目】如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=8,BD=4,求DC的长.
【答案】解:∵∠C=∠E,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴ ![]() =
= ![]() ,
,
又∵AD:DE=3:5,AE=8,
∴AD=3,DE=5,
∵BD=4,
∴ ![]() =
= ![]() ,即
,即 ![]() .
.
∴DC= ![]() .
.
【解析】由对顶角相等,可得![]() =
=![]() ,又∠C=∠E,可得△ADC∽△BDE,又因为对应边的比相等,计算可得CD的值。
,又∠C=∠E,可得△ADC∽△BDE,又因为对应边的比相等,计算可得CD的值。
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目