题目内容
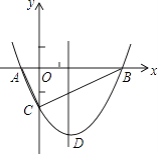
【题目】如图,点A、B在反比例函数 ![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
【答案】
(1)∵S△AOC=2,
∴k=2S△AOC=4;
∴y= ![]() ;
;
(2)解:连接AB,过点B作BE⊥x轴, 
S△AOC=S△BOE=2,
∴A(a, ![]() ),B(2a,
),B(2a, ![]() );
);
S梯形ACEB= ![]() (
( ![]() +
+ ![]() )×(2a﹣a)=3,
)×(2a﹣a)=3,
∴S△AOB=S△AOC+S梯形ACEB﹣S△BOE=3.
【解析】(1)根据反比例函数系数k的几何意义,可知S△AOC=![]() |k|,由图像可知k>0,即可求出反比例函数的解析式。
|k|,由图像可知k>0,即可求出反比例函数的解析式。
(2)连接AB,过点B作BE⊥x轴, 观察图像可知S△AOB=S△AOC+S梯形ACEB﹣S△BOE。根据反比例函数系数k的几何意义,可知S△AOC=S△BOE=2,只需求出梯形ACEB的面积,根据A、B两点的坐标及梯形的面积公式易求出它的面积,从而可求得结果。
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对比例系数k的几何意义的理解,了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目