题目内容
【题目】乘法公式的探究及应用.
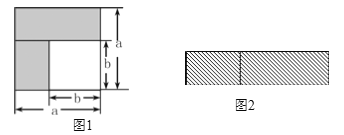
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
【答案】(1)a2 -b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a﹣b)=a2 ﹣b2;(4)①4m2 -n2 +2np-p2;②99.91.
【解析】
(1)利用面积公式:大正方形的面积-小正方形的面积=阴影面积;
(2)根据图1可得矩形的长和宽,然后利用矩形面积公式进行求解即可;
(3)利用面积相等列出等式即可;
(4)①先分组,然后利用平方差公式简便计算即可;
②写成两个数的和与两个数的差的形式,然后利用平方差公式简便计算即可.
(1)利用正方形的面积公式可知:阴影部分的面积=a2 -b2,
故答案为:a2 -b2;
(2)由图可知矩形的宽是a-b,长是a+b,面积是(a+b)(a-b),
故答案为:a-b,a+b,(a+b)(a-b);
(3)由阴影部分的面积不变可得(a+b)(a﹣b)=a2 ﹣b2,
故答案为:(a+b)(a﹣b)=a2 ﹣b2;
(4)①原式=[2m+(n-p)][2m-(n-p)] =(2m)2 -(n-p)2 =4m2 -n2 +2np-p2;
②原式=(10+0.3)×(10-0.3)=102 -0.32=100-0.09=99.91.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目










