Question

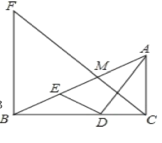
【题目】已知△ABC为等腰直角三角形，∠ACB＝90°，点A在直线DE上，过C点作CF⊥DE于F，过B点作BG⊥DE于G．

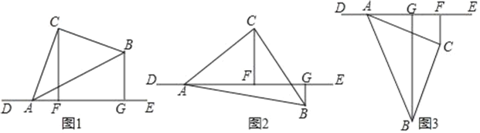
（1）发现问题：如图1，当B、C两点均在直线DE上方时，线段AG、BG和CF存在的数量关系是　 　．

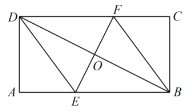
（2）类比探究：当△ABC绕点A顺时针旋转至图2的位置时，线段AG、BG和CF之间的数量关系是否会发生变化？如果不变，请说明理由；如果变化，请写出你的猜想，并给予证明；

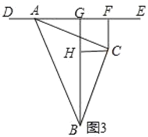
（3）拓展延伸：当△ABC绕点A顺时针旋转至图3的位置时，若CF＝1，AG＝2，请直接写出△ABC的面积．

Answer 1

【答案】（1）AG＝2CF﹣BG，（2）AG＝2CF+B；（3）5

【解析】

（1）过点B作BH⊥CF于点H，先判定四边形BGFH是矩形，再证△ACF≌△CBH，可得CH＝AF，BH＝CF＝FG，所以AG＝AF+FG，故AG＝AF+CF＝CH+CF＝CF+CF﹣HF＝2CF﹣BG；

（2）思路同上；

（3）过点C作CH⊥BG于H，先判定四边形BGFH是矩形，再证△ACF≌△BCH，CH＝CF＝GF＝1，AF＝AG+GF＝3，再利用勾股定理可得先判定四边形BGFH是矩形，AC＝CB=，最后算面积即可.

解：（1）发现问题：

如图1，过点B作BH⊥CF于点H，

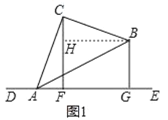
∵BH⊥CF，BG⊥AE，CF⊥AE，

∴四边形BGFH是矩形，

∴BH＝FG，FH＝BG，

∵△ABC为等腰直角三角形，

∴AC＝BC，∠ACB＝90°，

∴∠ACF+∠FCB＝90°，且∠FCB+∠CBH＝90°，

∴∠ACF＝∠CBH，且AC＝BC，∠AFC＝∠BHC＝90°，

∴△ACF≌△CBH（AAS），

∴CH＝AF，BH＝CF＝FG，

∵AG＝AF+FG，

∴AG＝AF+CF＝CH+CF＝CF+CF﹣HF＝2CF﹣BG；

故答案为：AG＝2CF﹣BG，

（2）类比探究：

数量关系发生改变，AG＝2CF+BG

理由如下：

如图2，过点B作BH⊥CF于H，

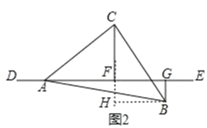
∵BH⊥CF，BG⊥AE，CF⊥AE，

∴四边形BGFH是矩形，

∴BH＝FG，FH＝BG，

∵△ABC为等腰直角三角形，

∴AC＝BC，∠ACB＝90°，

∴∠ACF+∠FCB＝90°，且∠FCB+∠CBH＝90°，

∴∠ACF＝∠CBH，且AC＝BC，∠AFC＝∠BHC＝90°，

∴△ACF≌△CBH（AAS），

∴CH＝AF，BH＝CF＝FG，

∴AG＝AF+FG＝CH+BH＝CF+FH+CF＝2CF+BG；

（3）拓展延伸：

如图3，过点C作CH⊥BG于H，

∵CH⊥BG，BG⊥AE，CF⊥AE，

∴四边形CHGF是矩形，

∴CH＝FG，CF＝GH，∠FCH＝90°，

∵△ABC为等腰直角三角形，

∴AC＝BC，∠ACB＝90°＝∠FCH，

∴∠ACF＝∠BCH，且AC＝BC，∠AFC＝∠BHC＝90°，

∴△ACF≌△BCH（AAS），

∴CH＝CF＝GF＝1，

∴AF＝AG+GF＝3，

∴AC＝CB＝＝＝，

∴S△ABC＝×AC×BC＝5．