题目内容
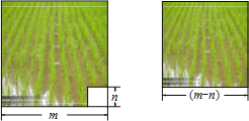
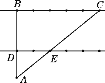
【题目】某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1．在温室内，沿前侧内墙保留3m宽的空地，其它三侧内墙各保留1m宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是288m2？
【答案】解法一：设矩形温室的宽为xm，则长为2xm．根据题意，得
（x﹣2）（2x﹣4）=288．
解这个方程，得x1=﹣10（不合题意，舍去），x2=14．
所以x=14，2x=2×14=28．
答：当矩形温室的长为28m，宽为14m时，蔬菜种植区域的面积是288m2．
解法二：设矩形温室的长为xm，则宽为
xm．根据题意，得
（x﹣2）（x﹣4）=288．
解这个方程，得x1=﹣20（不合题意，舍去），x2=28．
所以x=28，x=×28=14．
答：当矩形温室的长为28m，宽为14m时，蔬菜种植区域的面积是288m2．
【解析】本题有多种解法．设的对象不同所列的一元二次方程不同．一般情况下当两个量之比为a：b时，则设它们分别为ax和bx.
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x＋40 | 90 |
每天销量（件） | 200－2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元[
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.
